🔴 ¿Cómo resolver una raíz cuadrada de cuatro cifras sin usar calculadora?

Para ello situamos el número del cual queremos calcular su raíz -en nuestro caso el 5343- dentro de una línea quebrada, llamada RADICAL, con la forma mostrada en la imagen, situando dicho número en la zona del RADICANDO y dividiendo dicha línea con una vertical que separará en la misma franja horizontal, dicho radicando del resultado final, es decir, de la RÁIZ.

Bajo el Radicando iremos situando las líneas auxiliares de cálculo o "renglones auxiliares" que serán básicamente restas (diferencias).  Bajo la Raíz se irán colocando las multiplicaciones, como iremos viendo en el resto del procedimiento.

Vemos en la figura que existe el número 2 en la zona del quiebro de la línea que se denomina ÍNDICE y nos indica que buscamos la "RAÍZ CUADRADA".  En caso de que buscásemos una "raíz cúbica" el índice sería el 3 y así otras raíces más complejas.

Para este caso hemos tomado un número de 4 CIFRAS que no nos proporciona una solución entera en su raíz cuadrada, es decir, que obtendremos decimales que a efectos de aprendizaje de raíces cuadradas, nos ayudará a consolidar su resolución y saber cómo tratar el cálculo de los números decimales del resultado.

¿Cómo empezar a calcular una raíz cuadrada de un número de 4 cifras? © Raizcuadrada.de

De esta forma nuestro número objeto del cálculo de su raíz quedará dividido gráficamente a efectos de ayudarnos en el cálculo en los pares: 53 y 43, como podemos ver en la imagen anterior.

¿Cuál es el número de 1 a 9 que multiplicado por sí mismo es menor o igual al primer par (53)?

En estos casos siempre es más que recomendable tener la siguiente tabla a mano:

Se trata de la tabla de cuadrados de los números del 1 al 9 y son muy útiles para el cálculo de raíces con este método.  Es muy probable que no la necesites si sabes bien las tablas de multiplicar ya que se trata del producto de un número por sí mismo, pero nunca está de más tenerla a mano, cuando calcules raíces cuadradas.

Para nuestro caso buscamos un número del 1 al 9 que al multiplicarlo por sí mismo sea igual o menos a 53.  Si pensamos un poco podemos ver que el 8 podría ser un candidato a ser ese número buscado pero 8 * 8=64, lo que implica que se pasa.

Probemos con el 6: 6 * 6=36.  Parece que se nos queda un poco corto, con lo que nos queda probar el 7: 7 * 7=49.  Dado que el 8 ya hemos visto que se queda por encima y el 7 con el 49 de su cuadrado está por debajo, podemos concluir que el número que buscamos es el 7.

Así que ya tenemos el primer dígito de nuestra solución por su parte derecha y entera: el 7.

Primer dígito de la solución que buscamos para esta raíz cuadrada © Raizcuadrada.de

Obtenida esa primera cifra que formará parte del resultado, es decir de la raíz de 5343, vamos a situarnos bajo el Radicando en la zona de los Renglones Auxiliares para colocar bajo el 53 el cuadrado de "7", es decir, 49 que hemos calculado en la fase anterior.

De entre 53 y 49 debemos calcular su diferencia, que nos permitirá entender porque en el paso 3 buscábamos que el número cuadrado buscado fuese igual o menor, para evitar que la diferencia nos generase un número negativo.  Dicha diferencia, como vemos en la imagen es 4, que situamos en la línea inferior al 49.  Sería el primer resto (residuo) que obtenemos pero aún no hemos terminado.

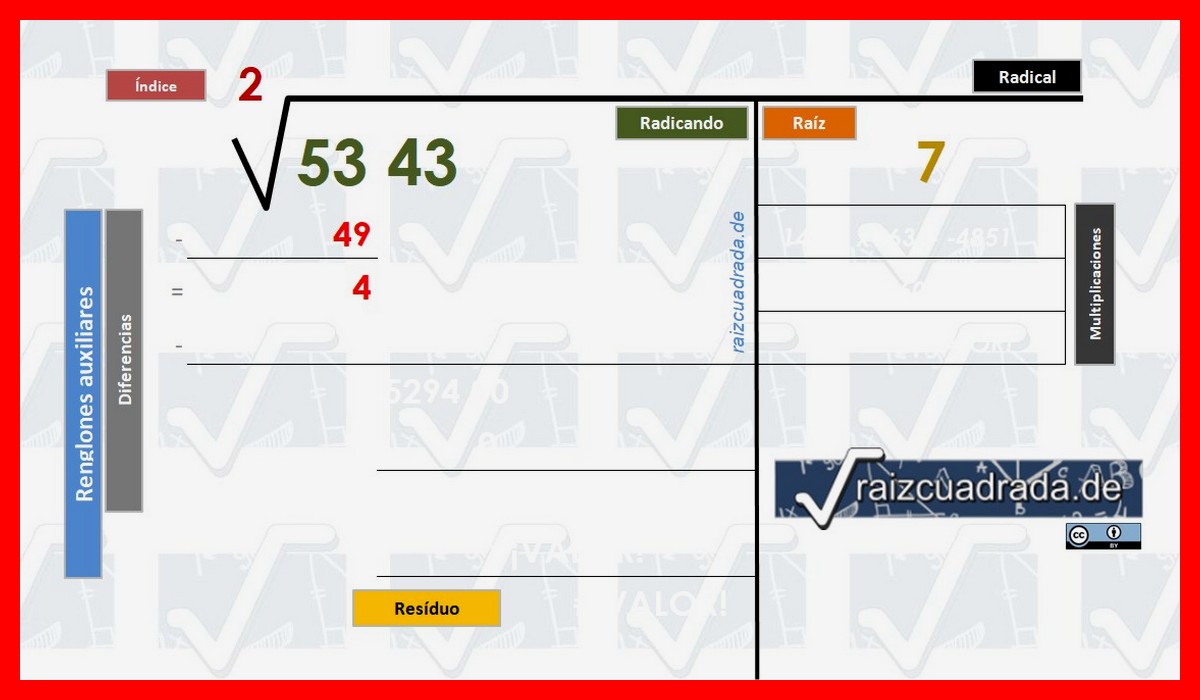
Obtenemos el primer residuo de esta raíz cuadrada pero debemos seguir para obtener toda la solución de 2 decimales © Raizcuadrada.de

Junto al primer residuo obtenido "4", situamos (bajamos) el segundo par de cifras del número del que queremos calcular su raíz, en nuestro ejemplo el "43".  De esta forma nos quedará un número con el que trabajaremos en el siguiente paso, el 443.

Bajamos el 2º bloque de par de dígitos del radicando de 4 cifras del que buscamos su raíz cuadrada © Raizcuadrada.de

Volvemos a la columna de la derecha (bajo la Raíz) y situamos en la primera línea de multiplicaciones el doble del número que tenemos provisionalmente como Raíz, es decir el 7.  El doble de "7" es "14" el cual situaremos en esa 1ª línea de multiplicaciones auxiliares.

La dificultad ahora es la de encontrar un número "X" que al ponerlo junto al 14 y multiplicándolo ese "14X" por esa "X" obtengamos un número igual o inferior a 443.  Lo habitual en estos caso y cuando se tiene poca práctica es ir iterando (probando) de forma manual.  Primero con el "1": 141 * 1=141.  Probamos con el "2": 142 * 2 = 284.  Aún estamos lejos de los 443.  Probamos con el "3": 143 * 3 = 429.  Parece que hemos dado con el número buscado porque estamos a pocas unidades de 443 y el siguiente paso sería el "4" que con un cálculo mental rápido ya nos da a entender que superará fácilmente el 500.

Así que hemos llegado a nuestro objetivo: el número buscado es el "3" y el producto obtenido el 429.

Pero, ¿podríamos encontrar más fácilmente ese número sin tener que ir probando cado uno de los números del 1 al 9?.  La respuesta es "Sí" y lo llamaremos "EL TRUCO", porque volveremos a usarlo más adelante y nos referiremos así a él.

Para ello podríamos usar este pequeño truco: toma el 443 y divídelo por 140 que sería el número "14" con un cero (0) final.  Si haces dicha operación obtendrás el número 3,16... (casi el número PI, jejeje!) lo que nos indicará que el primer número con el que debemos probar es el "3".  No siempre será el número buscado pero se aproximará y en caso de que supere la cifra que tenemos como objetivo máximo en los "renglones auxiliares", solamente tendremos que quitar a este número una unidad, en nuestro caso, probar con el "2".

El resultado buscado, es decir la "raíz", ya va tomando forma y junto al "7" obtenido en le 3er paso, ya tenemos un nuevo número: el "3".  De esta forma la raíz hasta el momento sería igual a 73, pero aún nos queda algo de camino algorítmico por recorrer.

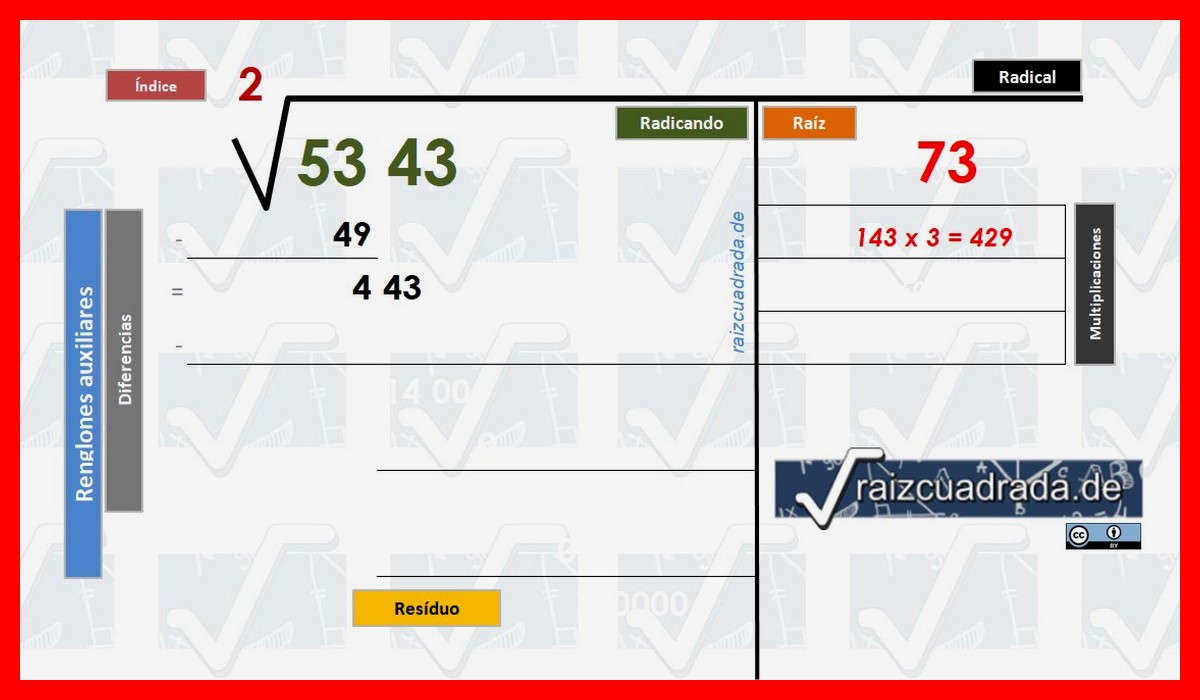
Encontramos el segundo número de nuestra solución para esta raíz © Raizcuadrada.de

En nuestra zona de "renglones auxiliares" bajo el Radicando llevamos a cabo la diferencia entre 443 y 429 que hemos obtenido en los pasos 5º y 6º.  Dicha diferencia será 14 que colocaremos debajo en una nueva línea auxiliar y llega el momento de empezar a trabajar con decimales...

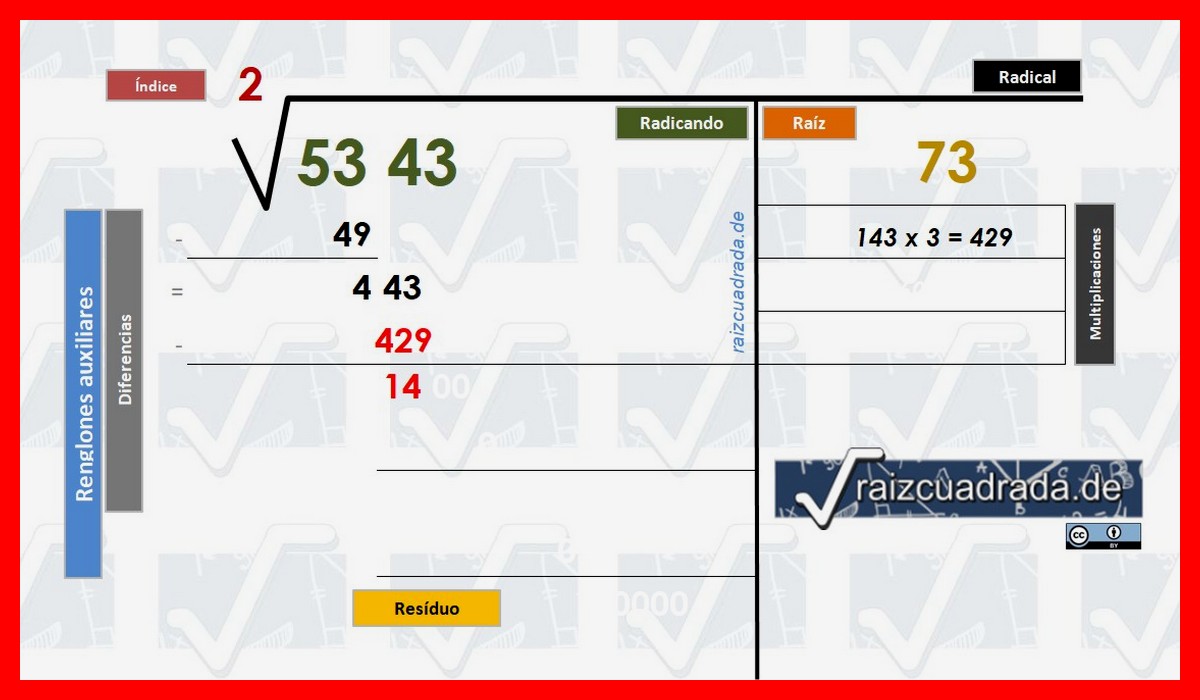
Calculamos la diferencia y obtenemos un nuevo residuo pero, ¿qué hacemos ahora para seguir para encontrar la solución más precisa? © Raizcuadrada.de

Si el residuo obtenido no hubiese sido 14 y sí "0" entonces estaríamos hablando de que el procedimiento estaría concluido y el resultado sería un número entero (sin decimales).  En nuestra web puedes encontrar muchos de estos caso haciendo click en la etiqueta "ENTERO" (click aquí), donde te mostramos muchísimos de estos números cuya raíz es un número entero.

Pero el ejemplo que llevamos entre manos no está entre los "elegidos" para una solución entera y sí para una solución con decimales.  Llega por tanto un momento importante y es qué hacer para seguir calculando los decimales correspondientes a la solución buscada.

En esta caso la respuesta es sencilla y podemos razonarlo de la siguiente forma y que que todo número entero es un número con "infinitos" decimales igual a cero cada uno de ellos.  Es decir que nuestro número de partida sería el: 5343,00 00 00 00 00.....00 00 00 00 00.  Partiendo de esta "licencia memorística" ya podemos intuir qué hacer cuando debemos seguir calculando los decimales en nuestro proceso algorítmico.

En este caso deberíamos bajar de nuevo un par de cifras que los bloques de 2 que habremos hecho con los decimales del Radicando a partir de la coma.  De esta forma estamos aprendiendo también, indirectamente, a cómo podríamos calcular la raíz cuadrada de un número con cifras decimales.  Volviendo a nuestro ejemplo, ahora deberíamos bajar al renglón auxiliar 2 ceros "00" y situarlos junto al número "14", nuestro residuo anterior.

Nos quedaría la cifra de 1400 esperando que continuemos nuestros cálculos.

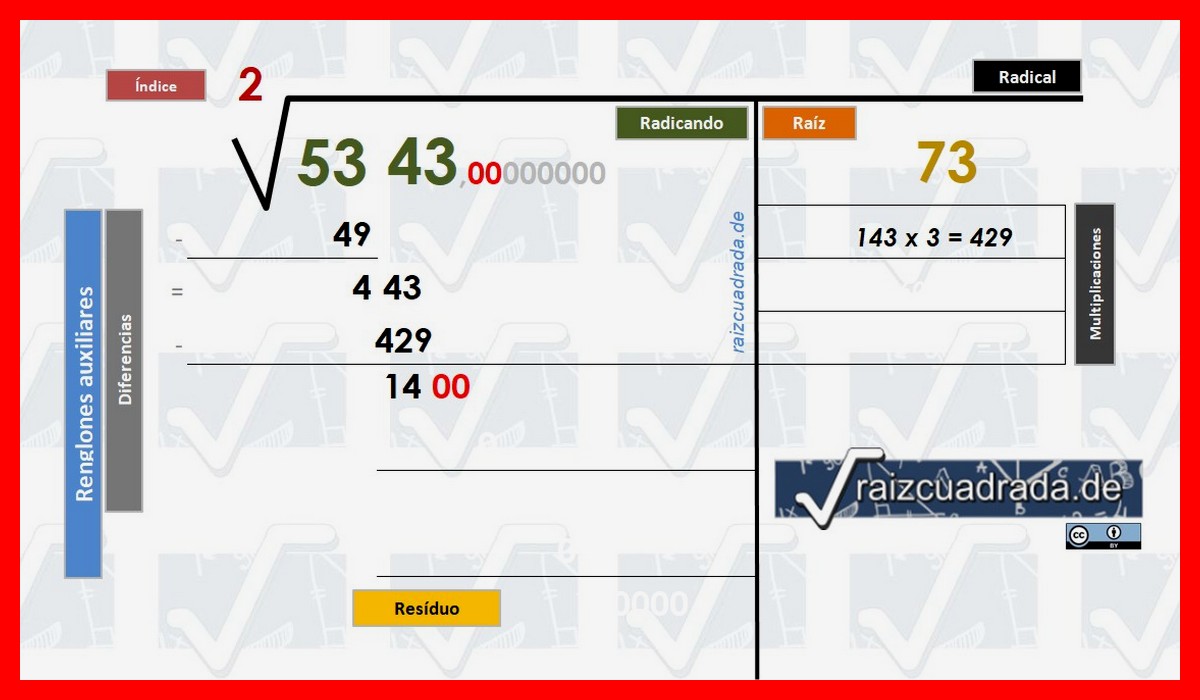
Empiezan los cálculos para obtener la parte decimal de la solución buscada © Raizcuadrada.de

Repitiendo un proceso similar al punto 6º debemos situar en la 2ª línea de multiplicaciones el doble del número 73 que es el resultado hasta ahora conseguido para este procedimiento.  De esta forma el número a situar en dicha línea auxiliar de multiplicaciones es el 146.

Ahora debemos volver a razonar como en dicho punto 6 y buscar qué número "X" situado junto al 146 X y multiplicando dicha cifra por dicho número "X" nos proporciona una cifra igual o inferior a 1400 obtenida en el paso anterior.

Aquí podríamos volver a usar el TRUCO del punto 6º pero tenemos que analizar qué pasa en realidad.  Para ello podríamos poner a 146 un CERO final y usar dicho número "1460" como divisor ante el 1400 de los renglones auxiliares.  Al llevar a cabo dicha división veríamos que el número obtenido no llega a 1 ya que el numerador es inferior al denominador.  Es el momento de pensar por un momento qué pasaría si no pusiésemos el "0" y sí el "1".  Entonces tendríamos que ver si 1461 * 1 = 1461 y, como podemos observar, es un número mayor que 1400, lo que hace que el "1" no sea válido ya que buscamos que sea igual o inferior.

¿Qué pasa ahora? ¿Qué podemos hacer? Al no ser válido el 1, debemos bajar un escalón y usar el "0".  Entonces operaríamos así: 1460 * 0 = 0, es decir que la multiplicación que buscamos en las líneas auxiliares bajo la Raíz es igual a CERO (0).

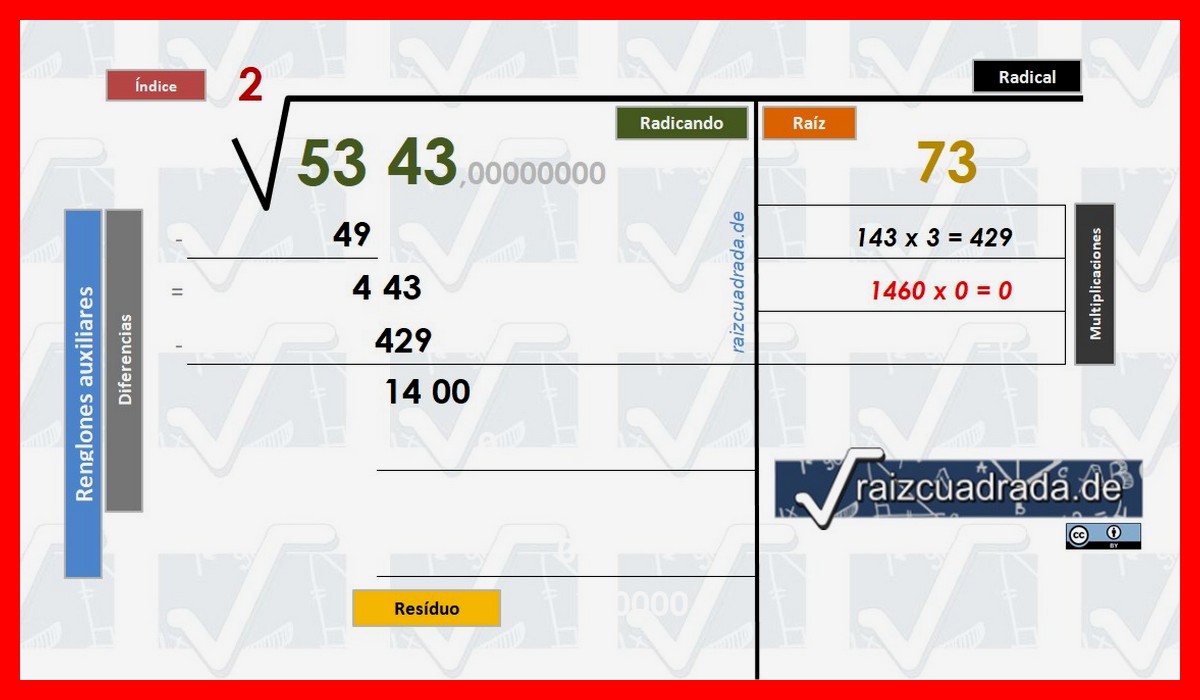
Primer decimal de solución a la raíz cuadrada que buscamos © Raizcuadrada.de

El haber encontrado el "0" como solución a nuestro paso 9º conlleva dos aspectos:

• La siguiente cifra de nuestra solución, es decir de la raíz cuadrada que buscamos es CERO pero debemos ser cautelosos y no situarlo detrás de la cifra solución que estamos obteniendo sin tener en cuenta una cosa: es nueva cifra es la primera cifra de la parte decimal de la solución.  Es por ello que debemos colocar una "COMA (,)" entre el "3" y el "0" y nuestra solución tendrá el aspecto provisional de "73,0".
• El CERO obtenido de la multiplicación de 1460 * 0 = 0 pasará a los renglones auxiliares bajo el 1400 del paso 8º y será el que empleemos para hacer la diferencia.

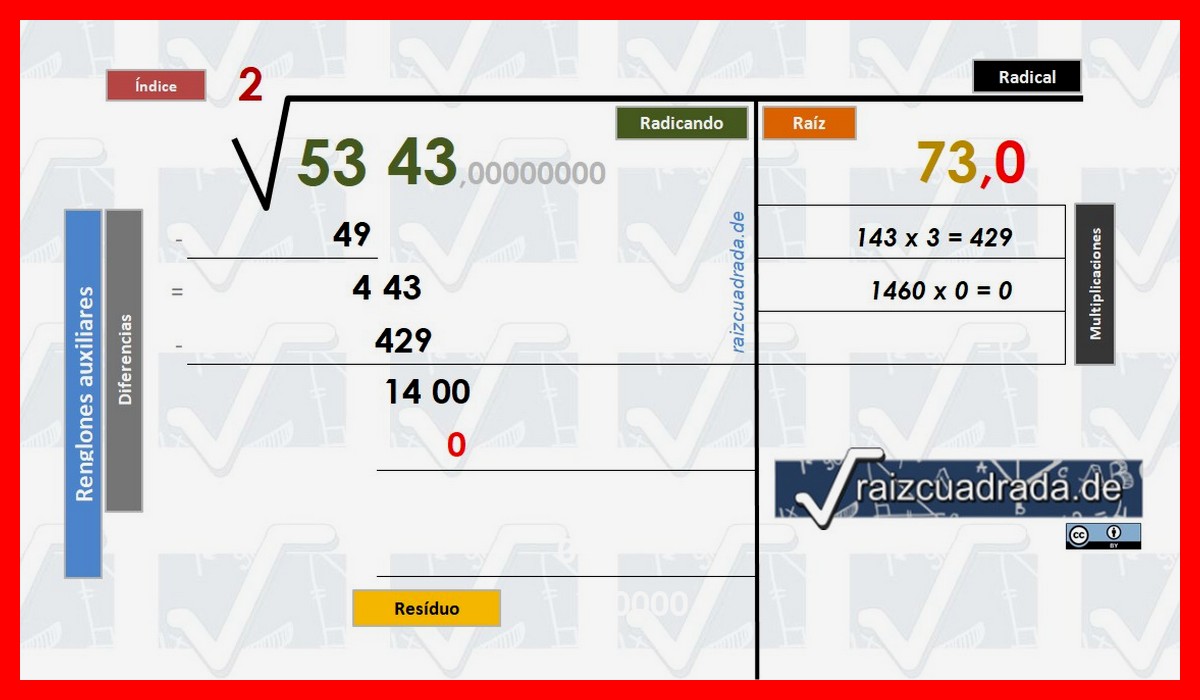
Primer decimal obtenido de la solución y previo a calcular el nuevo residuo del desarrollo para la raíz cuadrada © Raizcuadrada.de

Tal y como hemos visto en el punto anterior, la diferencia ahora en las líneas auxiliares bajo el Radicando será entre 1400 y 0, por lo que el resultado será 1400 y pasará a ocupar una nueva línea inferior auxiliar esperando el nuevo paso.

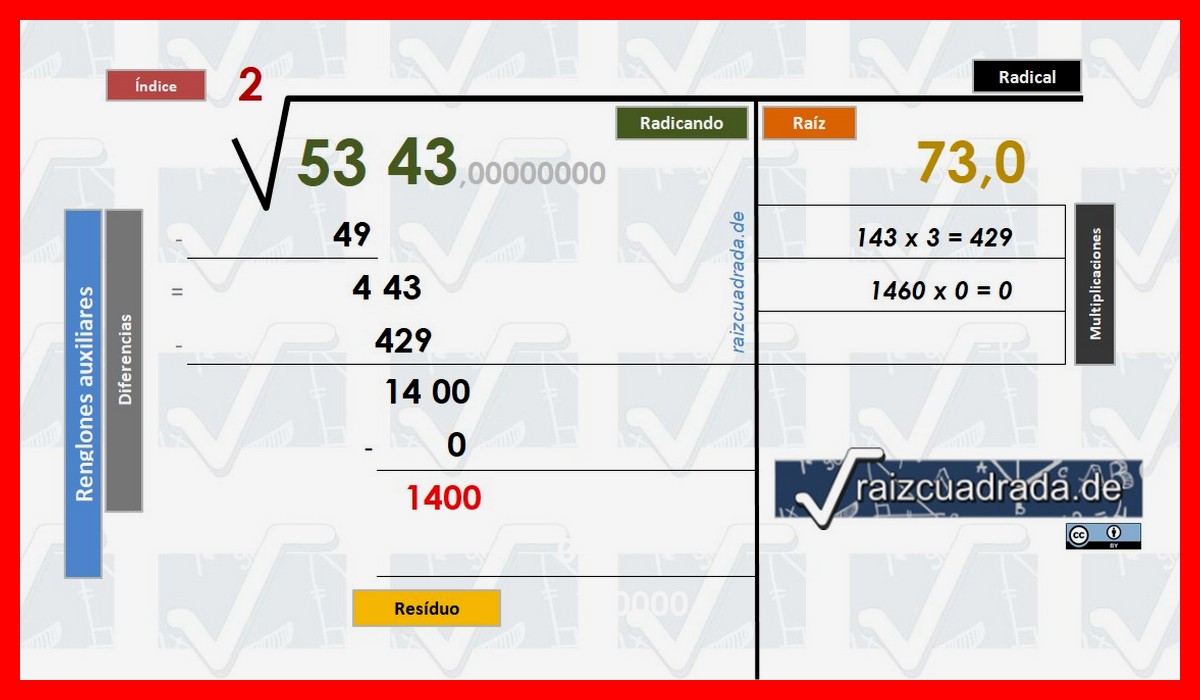
Residuo obtenido después de encontrar el primer decimal de nuestro resultado final © Raizcuadrada.de

Repitiendo lo comentado en le paso 8º, bajamos junto al 1400 del paso anterior un par de ceros procedentes de la parte "decimal" ficticia que hemos simulado para seguir calculando los decimales de esta raíz cuadrada.  De esta forma en ese renglón auxiliar abierto en el punto 11, tendremos una nueva cifra: 1400 00, preparada para el siguiente paso de cálculo iterativo.

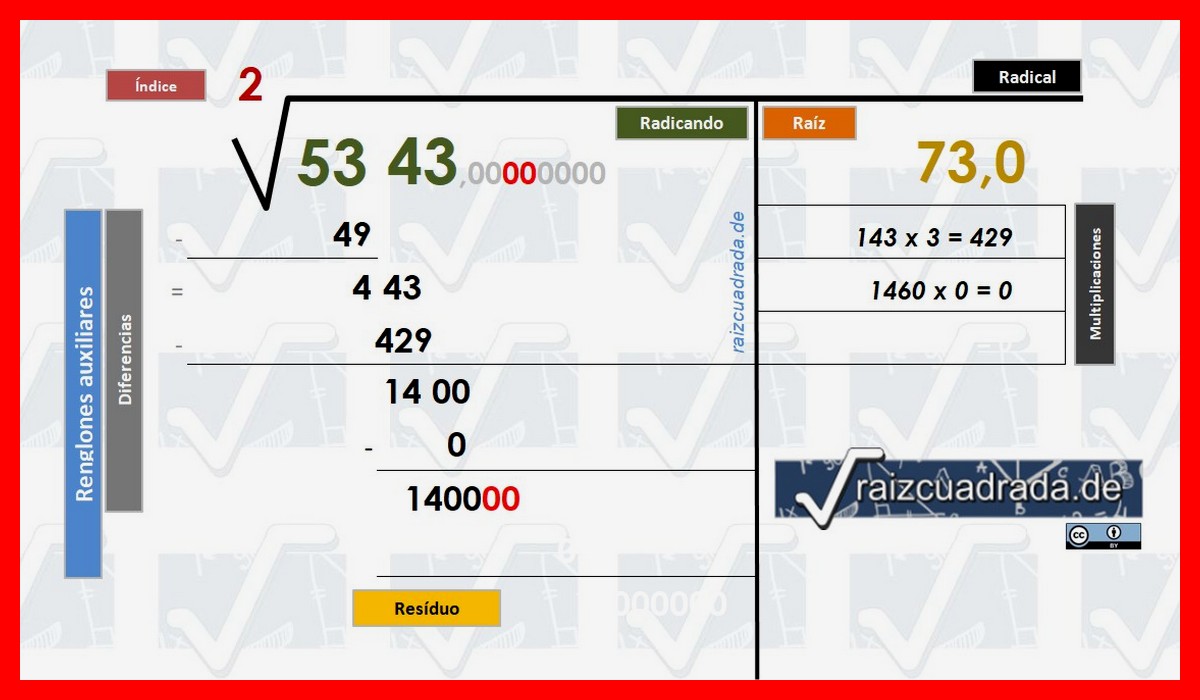
¿Cómo seguimos calculando nuestra raíz cuadrada para alcanzar la solución final? © Raizcuadrada.de

Ahora nos encontramos con un 140000 en la zona izquierda esperando que operemos sobre él, es decir que calculemos en la zona de multiplicaciones un número inferior o igual a él siguiendo los pasos ya descritos en los puntos 6º y 9º de este proceso.

Para ello vamos a calcular el doble de las cifras, sin considerar la coma, que actualmente tenemos como solución provisional de la Raíz.  Es decir debemos situar en una nueva línea auxiliar de multiplicaciones el doble de "730".  Con un rápido cálculo "x2" calculamos que el doble es "1460" y lo situamos en dicha línea de productos.

Como en pasos anteriores mencionados, ahora debemos encontrar un número "X" que al realizar la siguiente operación: 1460X * X nos dé un número igual o inferior a 140000.  Volvamos a usar el "TRUCO".

Así que la X será para nuestro "truco" un CERO: 14600 y dividiremos 140000 entre dicho 14600.  Realizando la operación obtenemos un 9,58 lo que nos indica que, es muy probable, que el número que buscamos sea el "9".  ¡Vamos a probarlo!

Si volvemos a 1460X * X y esa X creemos que es "9":  14609 * 9 = 131481 que como comprobamos fácilmente es un número inferior a 140000 y difícilmente puede ser otra la "X" buscada porque ya tendríamos que saltar al número "10" (esto no pasa nunca ya que buscamos siempre cifras entre 0 y 9) y la cifra obtenida en la multiplicación es superior a 140000.

Así que ya tenemos el número que buscábamos: el "9" y estamos muy cerca del final.

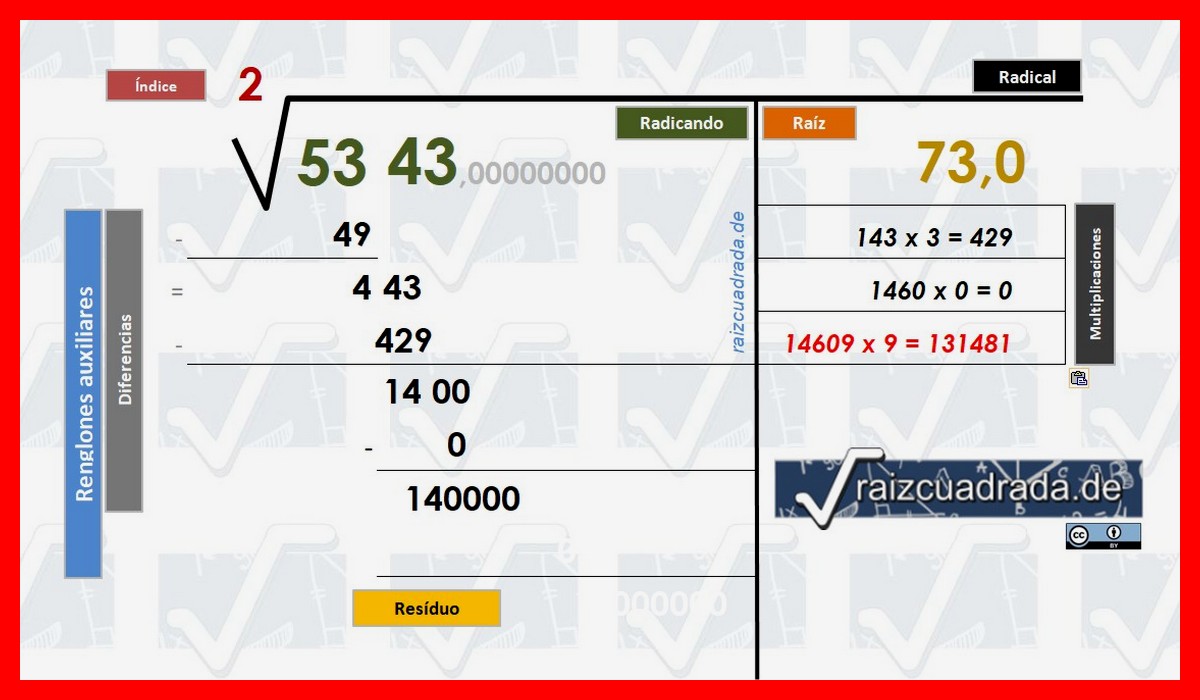
Ahora hacemos el proceso para calcular la segunda cifra decimal de nuestra solución raíz © Raizcuadrada.de

Efectivamente, gracias al paso anterior, ya hemos encontrado la raíz cuadrada de 5343, al menos, con 2 cifras decimales.  Para ello no quedaría más que poner junto a los 3 dígitos que ya teníamos el "9" obtenido y nuestra solución sería 73,09 pero: ¿sería estrictamente la solución buscada?

Sabemos que las Matemáticas son una ciencia muy precisa y siempre es bueno puntualizar los resultados.  De hecho si probásemos a calcular el cuadrado de 73,09: (73,09)² observaríamos que la solución obtenida sería casi 5343 pero no 5343: 5342,1481.

Esa imprecisión se debe a que arrastramos o tenemos un Residuo y deberíamos terminar nuestro proceso calculándolo.

Ya tenemos la solución completa con 2 decimales de nuestra raíz cuadrada pero, ¿es realmente precisa? © Raizcuadrada.de

Para ello debemos hacer la última diferencia dentro de nuestro proceso bajando a un nuevo renglón auxiliar el producto obtenido en el paso 13º y calculando la resta con el 140000.  De esta forma obtendremos el número 8519 que como podemos ver en la siguiente imagen, pasará a ser el Residuo final de nuestra operación de cálculo de la raíz cuadrada de 5343.

Obtenemos el residuo final de la raíz cuadrada de este número de 4 cifras © Raizcuadrada.de

Dicho residuo deberíamos usarlo como parte de la solución ante la pregunta de "¿Cuál es la raíz cuadrada de 5343?" ya que la respuesta correcta sería:

"La raíz cuadrada de 5343 es 73,09 con un residuo de 8519".

¿Cuál sería la solución precisa a nuestra raíz cuadrada? Dar el resultado e indicar cuál ha sido el residuo obtenido © Raizcuadrada.de